自适应卡尔曼滤波

最近一直在解决G474的ADC采样抖动问题，找到了卡尔曼滤波来过滤数据，先展示下效果：

/卡尔曼滤波,将ADC数据滤波再计算。
int KalmanFilter_Vin(int inData)
{
		static float prevData = 0.0F;                                 //先前数值
		static float p = 10.0F, q = 0.0001F, r = 0.05F, kGain = 0.0F;      // q控制误差  r控制响应速度 
	
		p = p + q;
		kGain = p / ( p + r );                                     //计算卡尔曼增益
		inData = prevData + ( kGain * ( inData - prevData ) );     //计算本次滤波估计值
		p = ( 1.0F - kGain ) * p;                                     //更新测量方差
		prevData = inData;
		return inData;                                             //返回滤波值
}

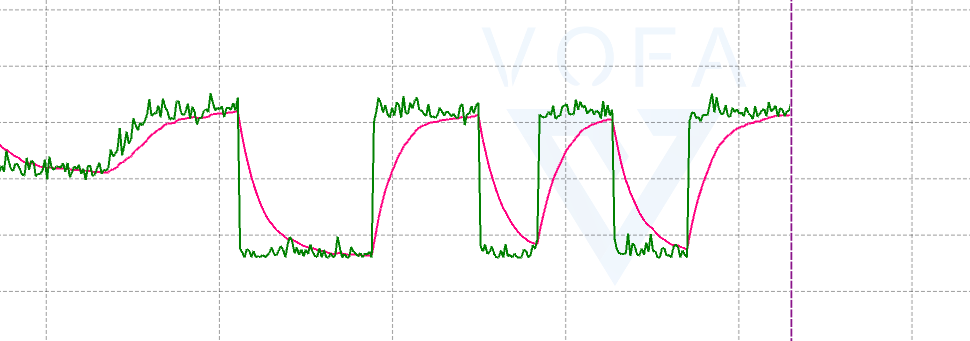
绿色为实时ADC读数，红色为卡尔曼滤波输出。

可以看出迟滞还是有点大，其实可以把r调大就可以加快相应速度，但是数据波动又会变大，所以我写了个自适应卡尔曼滤波函数：

#define THRESHOLD 60  // 设定一个阈值，用于判断数据变化是否剧烈
#define Q_MIN 0.001f    // 增大 q 的最小值
#define R_MAX 100.0f   // 限制 r 的最大值
#define KGAIN_MIN 0.01f // 限制卡尔曼增益的最小值
#define KGAIN_MAX 0.99f // 限制卡尔曼增益的最大值
#define STABLE_THRESHOLD 15  // 数据稳定的阈值
#define STABLE_COUNT_THRESHOLD 15  // 数据连续稳定的次数阈值

int KalmanFilter(int inData, float *prevData, float *p, float *q, float *r, int *stableCount)
{
    int diff = inData - *prevData;
    if (diff > THRESHOLD || diff < -THRESHOLD) {
        // 数据变化剧烈，增大 q 或减小 r 以提高响应速度
        *q *= 5.0f;
        *r /= 5.0f;
        *p += 10.0f;
        *stableCount = 0;
    } else {
        if (abs(diff) < STABLE_THRESHOLD) {
            (*stableCount)++;
            if (*stableCount >= STABLE_COUNT_THRESHOLD) {
                // 数据连续稳定，停止调整参数
            } else {
                // 数据变化缓慢，减小 q 或增大 r 以减小数据跳动
                *q /= 2.0f;
                if (*q < Q_MIN) {
                    *q = Q_MIN; // 限制 q 的最小值
                }
                *r *= 2.0f;
                if (*r > R_MAX) {
                    *r = R_MAX; // 限制 r 的最大值
                }
            }
        } else {
            *stableCount = 0;
            // 数据变化缓慢，减小 q 或增大 r 以减小数据跳动
            *q /= 2.0f;
            if (*q < Q_MIN) {
                *q = Q_MIN; // 限制 q 的最小值
            }
            *r *= 2.0f;
            if (*r > R_MAX) {
                *r = R_MAX; // 限制 r 的最大值
            }
        }
    }

    // 防止 p 溢出
    if (*p > FLT_MAX - *q) {
        *p = FLT_MAX - *q;
    }
    *p = *p + *q;

    float kGain = *p / (*p + *r);
    // 限制卡尔曼增益的范围
    if (kGain < KGAIN_MIN) {
        kGain = KGAIN_MIN;
    } else if (kGain > KGAIN_MAX) {
        kGain = KGAIN_MAX;
    }

    inData = *prevData + (kGain * (inData - *prevData));
    *p = (1.0f - kGain) * *p;
    *prevData = inData;
		
    return inData;
}

实际测试：

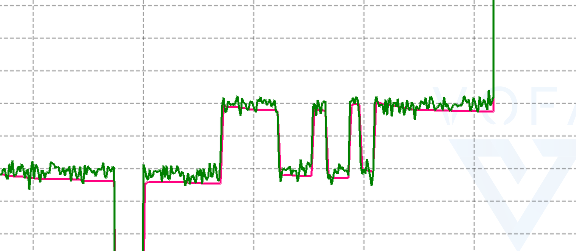
可以看出实时性很好。