之前在使用卡尔曼滤波确实数据稳定了,但是我是要测量1-60V的电压,量程比较大,我想精确到0.1V的量程所以将ADC超采样到13Bit让单片机精度更高一点。经过测试滑动平均滤波可以做到很好的实时性和数据稳定性
滑动平均滤波代码:
ADCVin = (uint32_t)vi_values[3];
VinAvgSum = VinAvgSum + ADCVin - (VinAvgSum >> 3); // 求和,新增入一个新的采样值,同时减去之前的平均值。
ADCVinavg = VinAvgSum >> 3; // 求平均现在输入的数据可以确定稳定了就可以校准数据了。
校准数据我找到的参考程序是使用线性校准但是我不知道为什么我查不到怎么算k值我只查到了
y=ax+b拟合算法来算,然后我就做了一张表来标定我的输入adc:
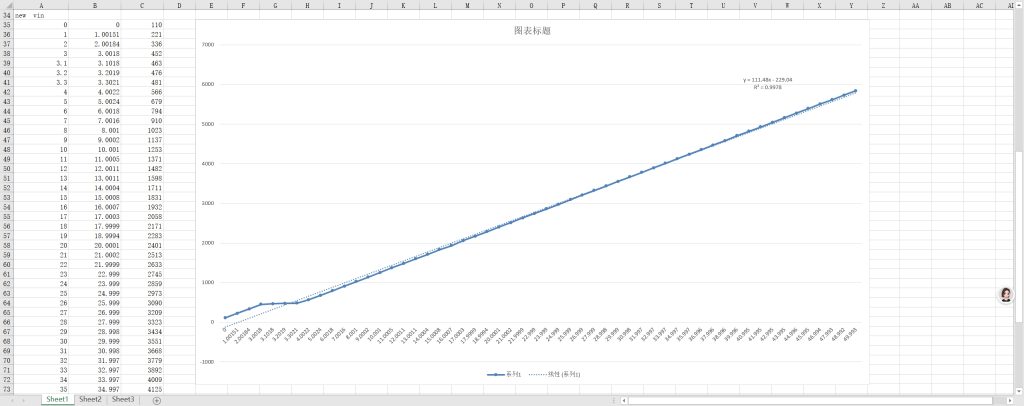
然后导入python脚本里运行得出结果:
import numpy as np
import matplotlib.pyplot as plt
x = np.array([0,
1.00151,
2.00184,
3.0018,
3.1018,
3.2019,
3.3021,
4.0022,
5.0024,
6.0018,
7.0016,
8.001,
9.0002,
10.001,
11.0005,
12.0011,
13.0011,
14.0004,
15.0008,
16.0007,
17.0003,
17.9999,
18.9994,
20.0001,
21.0002,
21.9999,
22.999,
23.999,
24.999,
25.999,
26.999,
27.999,
28.998,
29.999,
30.998,
31.997,
32.997,
33.997,
34.997,
35.997,
36.996,
37.996,
38.996,
39.996,
40.995,
41.995,
42.995,
43.995,
44.996,
45.995,
46.994,
47.993,
48.992,
49.993
])
y = np.array([110,
221,
336,
452,
463,
476,
481,
566,
679,
794,
910,
1023,
1137,
1253,
1371,
1482,
1598,
1711,
1831,
1932,
2058,
2171,
2283,
2401,
2513,
2633,
2745,
2859,
2973,
3090,
3209,
3323,
3434,
3551,
3668,
3779,
3892,
4009,
4125,
4237,
4353,
4466,
4579,
4704,
4814,
4928,
5044,
5159,
5273,
5390,
5506,
5611,
5727,
5841
])
def linear_least_squares_fit(x, y):
"""
执行最小二乘线性拟合
:param x: 输入电压数组
:param y: ADC 码值数组
:return: 斜率和截距
"""
n = len(x)
sum_x = np.sum(x)
sum_y = np.sum(y)
sum_xy = np.sum(x * y)
sum_x_squared = np.sum(x ** 2)
a = (n * sum_xy - sum_x * sum_y) / (n * sum_x_squared - sum_x ** 2)
b = (sum_y - a * sum_x) / n
return a, b
def polynomial_fit(x, y, degree):
"""
执行多项式拟合
:param x: 输入电压数组
:param y: ADC 码值数组
:param degree: 多项式的阶数
:return: 多项式系数
"""
coefficients = np.polyfit(x, y, degree)
return coefficients
def calculate_residuals(x, y, coefficients):
"""
计算残差
:param x: 输入电压数组
:param y: ADC 码值数组
:param coefficients: 拟合多项式的系数
:return: 残差数组
"""
poly = np.poly1d(coefficients)
y_pred = poly(x)
residuals = y - y_pred
return residuals
def calculate_r_squared(y, y_pred):
"""
计算决定系数 R^2
:param y: 实际值数组
:param y_pred: 预测值数组
:return: R^2 值
"""
ss_res = np.sum((y - y_pred) ** 2)
ss_tot = np.sum((y - np.mean(y)) ** 2)
r_squared = 1 - (ss_res / ss_tot)
return r_squared
# 线性拟合
a, b = linear_least_squares_fit(x, y)
print(f"线性拟合方程: y = {a:.2f}x + {b:.2f}")
y_linear_pred = a * x + b
linear_r_squared = calculate_r_squared(y, y_linear_pred)
print(f"线性拟合 R^2: {linear_r_squared:.4f}")
# 多项式拟合(二次)
poly_coeffs = polynomial_fit(x, y, 2)
poly = np.poly1d(poly_coeffs)
y_poly_pred = poly(x)
poly_r_squared = calculate_r_squared(y, y_poly_pred)
print(f"二次多项式拟合方程: {poly}")
print(f"二次多项式拟合 R^2: {poly_r_squared:.4f}")
# 计算残差
linear_residuals = calculate_residuals(x, y, [a, b])
poly_residuals = calculate_residuals(x, y, poly_coeffs)
# 绘制原始数据和拟合曲线
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.scatter(x, y, label='原始数据')
plt.plot(x, y_linear_pred, 'r-', label='线性拟合')
plt.plot(x, y_poly_pred, 'g--', label='二次多项式拟合')
plt.xlabel('输入电压 (V)')
plt.ylabel('ADC 码值')
plt.title('原始数据和拟合曲线')
plt.legend()
# 绘制残差图
plt.subplot(1, 2, 2)
plt.scatter(x, linear_residuals, label='线性拟合残差')
plt.scatter(x, poly_residuals, label='二次多项式拟合残差')
plt.axhline(y=0, color='k', linestyle='--')
plt.xlabel('输入电压 (V)')
plt.ylabel('残差')
plt.title('残差图')
plt.legend()
plt.tight_layout()
plt.show()得到结果:线性拟合方程: y = 114.84x + 104.70 线性拟合 R^2: 1.0000 二次多项式拟合方程: 2 0.0001346 x + 114.8 x + 104.8 二次多项式拟合 R^2: 1.0000
二次多项式解算对于单片机有点麻烦,先用线性拟合方程结算,套上公式解算:
Vin_true = ((ADCVinavg-104.70f)/ 114.84f);
if (Vin_true<0.9 | Vin_true>70) //防止零电压数乱飘
{
Vin_true = 0;
}看下效果:
发现的问题:线性度还不错,不过过了一会再测电压的时候差了0.1V,不知道为什么,感觉是零飘了,线性补偿的采样点一定要多,太小的话线性度不会特别好。
而且我没有查到我参考的程序的补偿值是如何算的,我的编程水平不高参考的程序好多移位看不太懂。哎。。。。




Comments NOTHING